What is Conditional Value at Risk (CVaR)?

In this previous post, we defined Value at Risk (VaR): given a time horizon $T$ and a level $\alpha$ , the VaR of an investment at level $\alpha$ over time horizon $T$ is a number or percentage X such that

Over the time horizon $T$ , the probability that the loss on the investment is $X$ or more is $1 - \alpha$ .

$\alpha$ -VaR is the $\alpha$ -quantile of $X$ , where $X$ is the distribution of the loss over time horizon $T$ .

Why looking at VaR isn’t enough

VaR helps us to understand the tail risk of the investment (in general the larger the VaR, the riskier the investment), but it doesn’t capture everything we need to know about tail risk. Consider two investments with the loss distributions shown in the figures below. Both of them have VaR at level 0.95 equal to 5. However, investment 1 can only lose up to 7% while investment 2 can lose up to 15%. In general most investors would prefer investment 1 to investment 2.

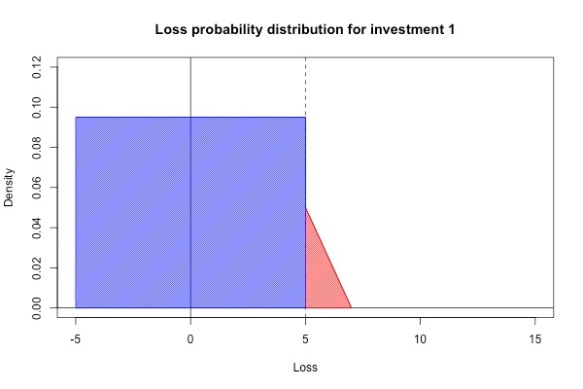
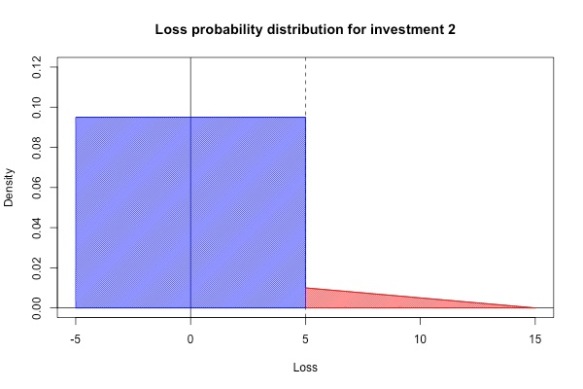Conditional Value at Risk (CVaR)

While VaR is unable to distinguish between the two investments above at the 95% level, conditional VaR (CVaR) is able to do so. Let’s call the tail risk a Conditional VaR at level $\alpha$ answers the question:

Let’s say I was unlucky and fell into the worst $1-\alpha$ of outcomes. Assuming that I’m in this set of bad outcomes, what is my expected loss?

In mathematical terms, CVaR is a conditional expectation: $\alpha$ -CVaR is the expected value of the loss conditional on the loss being greater than the $\alpha$ -VaR. If $X$ is the random variable for the loss and $q_\alpha (X)$ is the $\alpha$ -VaR, then

$\begin{aligned} \alpha\text{-CVaR} = \mathbb{E} \left[ X \mid X \geq q_\alpha (X) \right] .\end{aligned}$

In the example in the previous section, investment 1 had a 0.95-CVaR of $5 \frac{2}{3}$ while investment 2 had a 0.95-CVaR of $8\frac{1}{3}$ , which reflects our intuition that investment 2 is a riskier investment.

CVaR for common probability distributions

Norton et al. (2019) (Reference 3) provide formulas for some of the common probability distributions. Here are some of them (see the paper for the full list with proofs in the Appendix):

If $X$ has exponential distribution with rate parameter $\lambda$ , then

$\begin{aligned} \alpha\text{-CVaR} = \dfrac{-\log (1 - \alpha) + 1}{\lambda}. \end{aligned}$

If $X$ has Pareto distribution with shape parameter $a > 1$ and scale parameter $x_m$ , then

$\begin{aligned} \alpha\text{-CVaR} = \dfrac{x_m a}{(1 - \alpha)^{1/a}(a-1)}. \end{aligned}$

(If $a \in (0, 1]$ , then $\alpha\text{-CVaR} = \infty$ .)

If $X$ has Laplace distribution with location parameter $\mu$ and scale parameter $b$ , then

$\begin{aligned} \alpha\text{-CVaR} = \begin{cases} \mu + b \left( \frac{\alpha}{1-\alpha}\right) [1 - \log (2 \alpha)] &\text{if } \alpha < 1/2, \\ \mu + b \left[ 1 - \log [2(1-\alpha)] \right] &\text{if } \alpha \geq 1/2. \end{cases} \end{aligned}$

If $X$ has normal distribution with mean $\mu$ and variance $\sigma^2$ , then

$\begin{aligned} \alpha\text{-CVaR} = \mu + \sigma \dfrac{f \left( q_\alpha \left( \frac{X - \mu}{\sigma}\right) \right)}{1 - \alpha}, \end{aligned}$

where $f(\cdot)$ is the PDF of the standard normal distribution and $q_\alpha(\cdot)$ is the $\alpha$ -quantile of the standard normal distribution.

If $X$ has lognormal distribution with parameters $\mu$ and $s$ , then

$\begin{aligned} \alpha\text{-CVaR} = \dfrac{1}{2}e^{\mu + \frac{s^2}{2}} \dfrac{1 + \text{erf}\left( \frac{s}{\sqrt{2}} - \text{erf}^{-1}(2\alpha - 1) \right)}{1-\alpha}, \end{aligned}$

where $\text{erf}(\cdot)$ is the error function.

If $X$ has logistic distribution with location parameter $\mu$ and scale parameter $s$ , then

$\begin{aligned} \alpha\text{-CVaR} = \mu + \dfrac{s H(\alpha)}{1 - \alpha}, \end{aligned}$

where $H(\alpha) = - \alpha \log \alpha - (1-\alpha) \log (1-\alpha)$ is the binary entropy function.

If $X$ has $t$ -distribution with $\nu$ degrees of freedom, location parameter $\mu$ and scale parameter $s$ , then

$\begin{aligned} \alpha\text{-CVaR} = \mu + s \left( \dfrac{\mu + T^{-1}(\alpha)^2}{(\nu - 1)(1-\alpha)} \right) \tau \left( T^{-1}(\alpha)\right), \end{aligned}$

where $T^{-1}(\cdot)$ is the inverse of the standardized $t$ -distribution’s CDF (i.e. $\mu = 0$ and $s = 1$ ), and $\tau(\cdot)$ is the PDF of the standardized $t$ -distribution.